甲、乙两辆小车从相距100米的轨道两端同时出发相向而行，甲车以2米/秒的速度匀速行驶，乙车从静止状态开始以1米/秒²的加速度均匀加速行驶，到达终点后停下。问以下哪个图能准确描述甲乙各自到达终点前，两车之间的距离与时间的关系（横轴为时间，纵轴为直线距离）？

第一步：判断题型------本题为行程问题

第二步：分析作答
方法一：
甲的速度为2米/秒，乙的加速度为1米/秒2，由于乙的速度2秒后就能超过甲，因此乙车比甲车先到达终点并停止行驶，乙到终点后，两车之间的距离就是甲车离出发点的距离，即甲的行驶路程，则函数最后在坐标轴中表示为一条直线，排除B、C；且最后一段与开始时不可能对称，排除A。
故本题选D。

方法二：
甲车以2米/秒的速度匀速行驶，t秒行驶路程2t米；乙车从静止开始以1米/秒2的加速度匀加速行驶，由位移公式，可得乙车t秒行驶米。甲到达终点需要100÷2=50秒，乙车到达终点需要秒＜50秒，所以乙车先到达终点。由此我们可以将整个过程分为3段。
第一段是在两车相遇之前，两车的距离为，是一个二次函数，且开口向下，因为随着时间的推移距离越来越小，所以只保留对称轴右边的图像：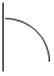
第二段是两车相遇后且在乙到达终点前，两车的距离为，是一个开口向上的二次函数。因为随着时间的推移距离逐渐拉大，所以只保留对称轴右边的图像：
第三段是当乙车到达终点时停止行驶，甲车仍继续行驶，此时两车之间的距离＝甲的路程=2t，是正比例函数，图像呈一条直线，且随着时间的推移距离越来越大直到甲车到达终点停止。
两车之间的距离与时间的函数由三部分组成：一段开口向下的抛物线，加一段开口向上的抛物线，再加一段直线。

故本题选D。
【2020-四川上-047】