某公园有一个圆形的湖，在湖的直径EB处有一座观光桥，横穿整个湖。园区在平行于观光桥的MN处建造了一片雕塑群，用以介绍中国古代礼仪与民俗，其长度等于湖的半径。某游客在湖边与观光桥上边走边欣赏湖中的雕塑群，走过了A、B、C、D四处位置。如图所示，A为该湖的圆心，N、D、C在一条线上，且ND⊥AB。那么在这四处位置，游客的观察视角大于45°的有（ ）处。（观察视角，即游客在该点处观看景物的视野张角，例如在D点处，其观察视角为∠MDN）

第一步：判断题型------本题为几何问题

第二步：分析解题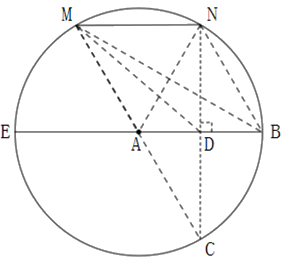

如上图所示，连接AM、AN、BM、BN、CM、DM，游客在A、B、C、D观察视角如下：
A点，MN长度等于湖的半径，则MN=AM=AN，△MAN是等边三角形，则∠MAN=60°＞45°；
B点，∠MBN、∠MAN是弧MN的圆周角、圆心角。根据圆周角定理“同弧所对的圆周角等于它所对的圆心角的一半”，则；
C点，∠MCN也是弧MN的圆周角，则∠MCN =30°＜45°；
D点，MN∥AB、ND⊥AB，则∠MND=90°，∠MDN+∠NMD=90°；在Rt△NAD中，AN＞ND，由于MN=AN，则MN＞ND，∠MDN＞∠NMD，则∠MDN＞45°。
综上，在A、B、C、D这四处位置，游客观察视角大于45°的是A、D点，共2处。

故本题选B。
【2023-上海A-037】