军事演习的模拟战场上有3个要点，B点在A点正北方3千米处，C点在A点正东方4千米处。现某部队保持与B、C两点相同的距离穿过战场，其在行进过程中，与A点之间最短的距离为多少千米：

A、

0.5

B、

0.6

C、

0.7

D、

0.875

参考答案： C

● 参考解析

第一步：判断题型------本题为几何问题

第二步：分析作答
根据题意，做出如下所示的图：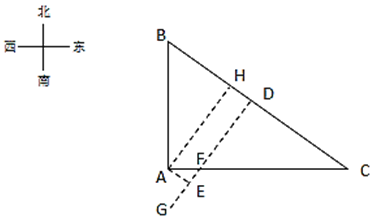
xiaomai
已知，AB=3千米，AC=4千米，由勾股定理得BC=5千米；
D是BC的中点，则CD=2.5千米。
要保持部队与B、C两点相同的距离穿过战场，则需过点D作DG⊥BC，DG所在直线即为部队的行进路线。
要求行进过程中与A点之间最短的距离，只需过点A作AE⊥DG，交DG于E，AE即为所求。
过点A作AH⊥BC，交BC于H，此时四边形AEDH为矩形，则AE=DH；
有相似性质可得：△BAC∽△AHC，，，解得CH=3.2。
则DH=CH-CD=3.2-2.5=0.7，即AE=0.7。

故本题选C。
【2018-北京-081】

当前位置：公务员＞国家公务员

军事演习的模拟战场上有3个要点，B点在A点正北方3千米处，C点在A点正东方4千米处。现某部队保持与B、C两点相同的距离穿过战场，其在行进过程中，与A点之间最短的距离为多少千米：

相关题目: